Оценка
вероятности знакомства с красивой и умной девушкой
На правах осеннего обострения
Данная работа посвящена анализу вопроса о существовании умных и
красивых девушек с точки зрения статистики. В ней производится аналитическая
оценка вероятности встретить такую девушку в общем виде, приводится пример
расчета вероятности для годового периода в России и описывается методика
подбора параметров. В заключении делается вывод о порядке этой величины, и
даются рекомендации по практическому решению данного вопроса.
С первого взгляда может показаться, что количественной оценки в данном случае дать нельзя, однако в данной работе будет продемонстрировано, что это не так. Начнем, конечно же, с формализации задачи, для этого нам потребуется расширить и дополнить изначальную формулировку вопроса до состояния, поддающегося количественному описанию.
Первое, что следует выяснить: временной интервал, для которого мы будем пытаться вычислить вероятность данного события. Временной интервал должен быть выбран достаточно большим для того, чтобы можно было применять статистический подход и, в то же время достаточно маленьким, для того чтобы в течение этого времени не слишком сильно изменялись основные социальные, культурные и личные характеристики участвующих в рассмотрении субъектов. Для простоты примем, что мы рассматриваем 1 год размеренной жизни одинокого субъекта примерно 20 лет, и в течение этого года не происходит никаких кардинальных перемен в его жизни.
Вторым пунктом следует определить, что же понимается под знакомством. Будем ли мы считать общение с новым продавцом соседнего магазина знакомством? Да, будем. Примем, что знакомством является акт взаимодействия с другим человеком, в результате которого у субъекта появляется возможность пообщаться с этим же человеком повторно без серьезных к тому препятствий, то есть контактная информация и согласие другого человека на продолжение общения.
Простейшие соображения также показывают, что для каждого отдельно взятого человека такой шанс будет различным и будет зависеть от ряда субъективных характеристик, и расчет такового для «среднестатистического человека» будет настолько же информативным, как и средняя температура по госпиталю. Таким образом, часть параметров будет приведена в общем виде, а также будет описана методика их количественного вычисления. С другой стороны, чтобы избежать расчета для «сферических людей в вакууме», за основу модели возьмем реальные статистические данные, соответствующие, в некоторой степени, реалиям нашей страны.
Подобная работа, с несколько иными изначальными посылками и качественно иным подходом к расчету была проведена Tristan Miller [1]. В ней была введена начальная выборка людей, к которой были последовательно применены фильтры. Хотя автор и не указывает на это прямо, последовательность применения этих фильтров имеет большое значение, т.к например распределение населения по возрастным группам сильно разнится от страны к стране и даже внутри страны может сильно «плавать» в зависимости от географических и культурных особенностей. Количество этих фильтров, таким образом, увеличивает погрешность полученного результата. Использование статистической выборки как основы прогноза предполагает равномерное распределение для вероятности выбора любого человека в полученном множестве. Такой подход позволяет получить некую полную усредненную вероятность, не учитывающую конкретной специфики того, для кого производится расчет. Отличия данной работы в том, что в ней не вводится начальная выборка, конечная вероятность зависит в большей степени от субъективных условий для испытателя, а количество используемых фильтров сведено к минимуму.
И, наконец, следует определить форму результата. Наиболее логичным, по мнению автора, будет результат в форме диапазона вероятностей для данного события на заданном промежутке времени. Получить его можно, последовательно применяя схему Бернулли для испытаний с двумя возможными исходами, задав наиболее и наименее выгодные параметры. Для этого следует определить вероятность положительного исхода элементарного события, оценить число испытаний и посчитать вероятность получения одного или более положительного исхода в серии.
Факторы успеха
Начнем с прикидки вероятности положительного исхода одного знакомства в общей форме. Положительный исход в нашей модели представляет собой знакомство с девушкой, подходящей под критерии «красивая» и «умная». Предполагается, что распределения и статистические выборки, используемые для расчета каждого из членов, являются, в первом приближении, взаимно независимыми.
![]()
В этой формуле:
Qi – коэффициент, характеризующий вероятность встретить умного человека,
Qmoe – коэффициент, характеризующий вероятность встретить красивого человека,
Qgirl – коэффициент, характеризующий вероятность встретить девушку,
kself – коэффициент, учитывающий прочие факторы, влияющие на положительный исход знакомства.
K0 – эмпирический поправочный коэффициент.
Все величины в этой формуле представляют собой неотрицательные действительные числа, все коэффициенты Q лежат в диапазоне (0;1].
Умная
Начнем с определения того, что же означает «умная девушка». Очевидно, что, в первую очередь, следует определить, относительно кого она должна быть умной. В первом приближении для количественной оценки интеллекта ограничимся тестом Айзенка для определения IQ. Поскольку для крупной выборки людей результаты теста подчиняются нормальному распределению[2], зададим кривую нормального распределения исходя из известных параметров для теста IQ: IQср = 100 и σ = 15.
В категорию умных попадают девушки, имеющие IQ больший, чем некоторое реперное значение, то есть нам нужно проинтегрировать область под кривой плотности вероятности справа от него. Репером, в данном случае, может служить IQ субъекта, для которого мы считаем вероятность, либо произвольно выбранный уровень IQ.
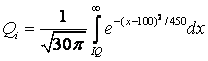
Поскольку интеграл вероятностей является трансцендентным, расчеты производятся численными методами.
Таблица 1. Qi для ряда значений IQ.
|
IQ |
Qi |
IQ |
Qi |
IQ |
Qi |
|
55 |
0,9986 |
90 |
0,7475 |
125 |
0,0478 |
|
60 |
0,9962 |
95 |
0,6306 |
130 |
0,0227 |
|
65 |
0,9902 |
100 |
0,5000 |
135 |
0,0098 |
|
70 |
0,9772 |
105 |
0,3694 |
140 |
0,0038 |
|
75 |
0,9522 |
110 |
0,2525 |
145 |
0,0014 |
|
80 |
0,9088 |
115 |
0,1587 |
|
|
|
85 |
0,8413 |
120 |
0,0912 |
|
|
Красивая
Этот фактор является наиболее субъективным в нашей модели, поэтому получить его значение аналитическим путем представляется трудной задачей, тем не менее, некую среднюю прикидочную оценку можно дать. По этой причине будет предложена как прикидочная аналитическая оценка этой величины, так и методология получения более корректной величины эмпирическим путем. Прикидочная оценка, как, в общем-то, и в предыдущем случае базируется на теореме Ляпунова[3], гласящей, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному.
Показатель красоты, выраженный численно, по всей видимости, будет подчиняться нормальному распределению на достаточно большой выборке случайных людей. Проблема заключается в том, что нам необходимо задать среднее значение и величину стандартного отклонения. Среднее значение примем для простоты равным 0, а касательно σ сделаем следующее замечание. Поскольку после выбора некоторого условного значения σ, нам также придется выбирать некую пороговую границу отбора для деления популяции на красивых и некрасивых, мы можем вообще не вводить численного значения для стандартного отклонения, а сразу выразить наши предпочтения в форме долей σ.
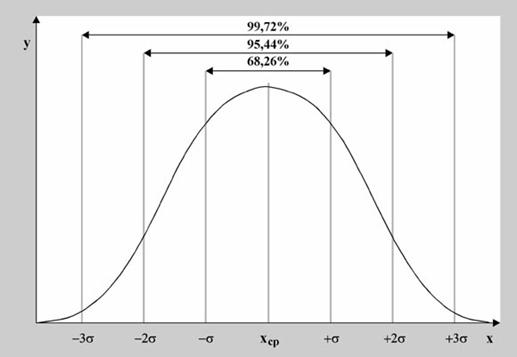
Рисунок 1. Вероятности попадания случайной величины в заданный
диапазон.
Чтобы как-то ограничить верхнюю и нижнюю границу для нашего выбора воспользуемся так называемым «правилом трех сигм»: пренебрежем вероятностью выхода величины за 3σ. Для 3σ это величина составляет ~0,27%. Теперь разобьем диапазон -3σ…3σ на 100 частей. Проще говоря, абстрагируемся от возможности существования «невероятно красивых» и «невероятно некрасивых» и выберем что-нибудь земное из таблицы 2. На шкале от 0 до 100 выбираем число N, которое будет определять нижнюю границу для численного выражения красоты, после этого находим Qmoe по формуле:
![]()
Знак “–” в случае N>50, “+” в случае N<50.
Таблица 2. Вспомогательная величина X для Qmoe.
|
|N-50| |
X(|N-50|) |
|N-50| |
X(|N-50|) |
|N-50| |
X(|N-50|) |
|N-50| |
X(|N-50|) |
|N-50| |
X(|N-50|) |
|
1 |
0,0239 |
11 |
0,2454 |
21 |
0,3962 |
31 |
0,4686 |
41 |
0,4931 |
|
2 |
0,0478 |
12 |
0,2642 |
22 |
0,4066 |
32 |
0,4726 |
42 |
0,4941 |
|
3 |
0,0714 |
13 |
0,2823 |
23 |
0,4162 |
33 |
0,4761 |
43 |
0,4951 |
|
4 |
0,0948 |
14 |
0,2995 |
24 |
0,4251 |
34 |
0,4793 |
44 |
0,4959 |
|
5 |
0,1179 |
15 |
0,3159 |
25 |
0,4332 |
35 |
0,4821 |
45 |
0,4965 |
|
6 |
0,1406 |
16 |
0,3315 |
26 |
0,4406 |
36 |
0,4846 |
46 |
0,4971 |
|
7 |
0,1628 |
17 |
0,3461 |
27 |
0,4474 |
37 |
0,4868 |
47 |
0,4976 |
|
8 |
0,1844 |
18 |
0,3599 |
28 |
0,4535 |
38 |
0,4887 |
48 |
0,4980 |
|
9 |
0,2054 |
19 |
0,3729 |
29 |
0,4591 |
39 |
0,4904 |
49 |
0,4984 |
|
10 |
0,2257 |
20 |
0,3849 |
30 |
0,4641 |
40 |
0,4918 |
50 |
0,5 |
Теперь об эмпирической методике проверки полученного теоретического значения. Для этого необходимо отмечать для себя число красивых прохожих и общее число оцененных. Отношение числа красивых к общему числу и представляет собой Qmoe, значение будет тем точнее, чем больше выборка. Такой метод, с одной стороны, много более трудоемок, по сравнению с теоретическим, а с другой позволяет получить различные значение коэффициента с привязкой к геоданным (что открывает новые перспективы, такие как подсчет удельной вероятности познакомится на квадратный метр поверхности). Кроме того, по наблюдениям автора, этот показатель также сильно зависит от времени года, так что для более объективных результатов следует опытным путем вычислить наименьший и наибольший Qmoe: Qmoe_min и Qmoe_max.
Девушка
Действительно, до сих пор речь шла о людях в целом, но в нашей задаче речь идет о девушках. Конечно, можно было бы просто задать этот множитель равным 0,5, но такое действие не совсем удачно отразит действительность. В этом разделе в качестве примера приведены статистические данные для России. Очевидно, что для получения более приближенных к действительности результатов следует использовать подобную статистику, но уже для конкретного региона или города, в котором проживает испытатель. С другой стороны, интернет и развитая система телекоммуникаций делает возможными также знакомства на большом расстоянии. Одним из возможных направлений развития модели является учет специфики конкретных методов знакомств и вклада каждого из них в общее количество знакомств испытателя.
… а возраст?
Если испытатель не является педофилом и/или геронтофилом, то разумно будет ввести в нашу модель некоторые ограничения на возраст, сверху и снизу. Воспользуемся для этого статистикой по возрастам для России на 2007 год[4].
Таблица 3. Распределение населения по
возрастным группам для России на
|
Возраст |
Население (n), тыс. человек |
Женщин на 1000 мужчин
соответствующего возраста (q) |
|
0-4 |
7223 |
948 |
|
5-9 |
6376 |
954 |
|
10-14 |
7283 |
957 |
|
15-19 |
11088 |
962 |
|
20-24 |
12671 |
977 |
|
25-29 |
11165 |
1002 |
|
30-34 |
10442 |
1018 |
|
35-39 |
9459 |
1031 |
|
40-44 |
10368 |
1076 |
|
45-49 |
12067 |
1121 |
|
50-54 |
10804 |
1205 |
|
55-59 |
8985 |
1289 |
|
60-64 |
4336 |
1449 |
|
65-69 |
7458 |
1696 |
|
70
и более |
12496 |
2429 |
Легко подсчитать, что если ограничиться возрастным диапазоном, например 15-34, то в него попадет только 31,9% от всего населения. Теперь, используя третий столбец, посчитаем, сколько в этом возрастном диапазоне будет девушек. Число довольно близко к ½ но чуть меньше: 49,74%. Общая формула, таким образом будет записана так:

где l, m – нижняя и верхняя границы возрастного ценза, ni – население России, попадающее в данную возрастную группу, а qi – количество женщин, приходящееся на 1000 мужчин данного возраста.
Уж замуж невтерпеж
Увы, но в жизни все далеко не так гладко как на бумаге. Сделаем несколько предположений, в частности, в первом приближении нашей модели будем считать, что особы женского пола, имеющие парня или мужа, будут не склонны к знакомству. Безусловно, это далеко не всегда верно, но статистических данных, позволяющих ввести поправочный коэффициент, у автора данной работы на данный момент нет. Чтобы до некоторой степени компенсировать неточность этого коэффициента, примем, что от знакомства откажутся только замужние женщины.
Таблица 4. Накопленная доля вступивших в первый брак к возрасту, %
|
Территория |
20 лет |
25 лет |
30 лет |
35 лет |
|
Россия |
38,5 |
80,2 |
90,2 |
93,6 |
|
Россия, русские |
39,1 |
80,4 |
90,2 |
93,5 |
Теперь, используя эти данные[5], внесем коррективы в формулу для Qgirl:

Мы умножаем количество девушек данного возраста на характерную долю незамужних, тем самым внося необходимую поправку. Как и в предыдущих случаях, для получения минимума и максимума вероятностей имеет смысл выбрать два возрастных диапазона, более узкий, предпочитаемый, и более широкий – допустимый.
А как насчет взаимности?
Итак, первые три коэффициента определены, но где гарантия, что с умной красивой девушкой удастся познакомиться? Существует ненулевой шанс, что при знакомстве, вместо ожидаемого положительного исхода, испытатель получит что-то в диапазоне от игнора до удара электрошоком включительно. К примеру, в один из дней написания этой статьи, девушка, зашедшая следом за автором в подъезд, предпочла подъем пешком до пятого этажа поездке с автором на лифте.
Нам нужно учесть этот параметр количественно, но он зависит в очень большой степени от данных самого испытателя. Личные наблюдения автора позволяют ему предложить в качестве первого приближения для этого параметра самооценку. Действительно, люди с заниженной самооценкой в силу чисто психологических причин имеют несколько меньший шанс произвести положительное впечатление на случайного человека. Для нашей модели примем, что такая зависимость имеет место быть и она линейная. Поэтому значение kself испытателю предлагается задать, дав самому себе оценку по десятибалльной шкале и поделить на 10. В некоторых особых случаях, вероятно возможны ситуации, когда умная красивая девушка сама знакомится с испытателем. Чтобы это учесть, особо успешным мачо предлагается задать kself большим единицы.
Конечно, kself можно разложить на составляющие и ввести отдельные численные коэффициенты для красоты испытателя, его коммуникационных качеств, обаяния и прочего, однако такой подход, по мнению автора, только вносит дополнительную погрешность из-за ярко субъективного характера этих показателей. Вычислить его обратным способом, исходя из результатов испытаний, тоже не представляется возможным, ввиду высокой вероятности «двойного учета» некоторых факторов в kself и k0 при таком подходе.
Известные недостатки модели, поправочный коэффициент
Главным недостатком модели не связанным с необходимостью использования субъективных оценок, что в данной ситуации неизбежно, можно считать принятие положения о том, что распределения и статистические выборки, параллельно используемые для расчета отдельных параметров, являются взаимно независимыми. Этот недостаток, как уже упоминалось выше, присутствует также в модели другого автора[1].
Если не использовать это положение, то будет иметь значение последовательность вводимых ограничений, при этом, правомерным будет только использование статистики для группы с подобными же ограничениями, использованными при подсчете, что определенно не представляется возможным в рамках данной работы. Другим вариантом решения этой проблемы является введение поправочных коэффициентов для каждого члена Q, что опять же требует эмпирического обоснования.
Проще говоря, нельзя с уверенностью сказать, что количество красивых девушек среди девушек умных также подчиняется нормальному распределению, распределение показателя красоты является нормальным для каждой из возрастных групп, а главное, как отличается процент замужних женщин среди умных и красивых от общей статистики. Коэффициент IQ, к счастью уже нормирован по возрасту, что немного упрощает задачу, остальные же взаимосвязи требуют дополнительных исследований.
Поскольку данных, позволяющих предложить даже общую форму для каждого из таких коэффициентов, нет, все они вынесены в единый поправочный коэффициент k0, некое эмпирическое значение которого можно получить опытным путем. На данном этапе примем k0 = 1, т.е. проигнорируем влияние факторов, указанных выше.
Серия знакомств
Зададим число испытаний, для чего воспользуемся усредненным числом знакомств в год. Этот важный показатель nenc каждый испытуемый может подсчитать для себя сам, учитывать следует всех новых людей, с которыми вы так или иначе впервые общались в течение года. Так как это может вызвать затруднения, можно подсчитать месячный показатель и аппроксимировать его на годичный, хотя, очевидно, что такой подход даст понижение точности. Как уже говорилось выше, для расчета диапазона значений вероятности имеет смысл выбрать две величины nenc_min и nenc_max,
Теперь, когда у нас есть все необходимые величины, посчитаем, используя схему Бернулли конечный результат, по минимуму и по максимуму. Для этого нам нужно найти какова вероятность получить 1 или более положительный исход в серии испытаний. Вероятность ровно m успехов в серии из n повторных независимых испытаний вычисляется по следующей формуле:
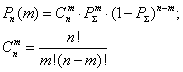
Для получения вероятности хотя бы одного положительного исхода требуется найти вероятность события, при котором испытатель получает ровно 0 положительных исходов в серии, и вычесть вероятность этого события из полной вероятности, т.е. 1. Простейшая подстановка показывает, что
![]()
Практическое применение модели
На нижеследующем примере расчета с последующим анализом проанализируем предсказательную мощь полученной модели. Для этого подставим в формулу 1.7 формулы 1.1-1.3 и 1.5:
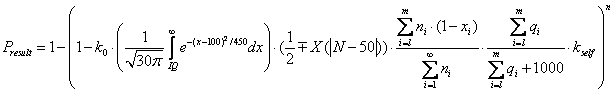
Подставим для каждого из членов параметры, соответствующие минимальному и максимальному результату:
Для IQ выберем значения 125 и 135, для граничного показателя красоты возьмем значения 80 и 90 соответственно, возрастной ценз установим в диапазонах 15-29 и 10-34 (осторожно, статья!), самооценку заявим как 7 и 8,5. Числа знакомств в год примем равными 10 и 35. Данные значения выбраны исключительно в демонстративных целях и сами по себе не следуют из каких-либо статистически достоверных данных, получение средних значений этих численных параметров для каких-либо социальных групп представляет собой отдельную задачу, не рассматриваемую в рамках этой работы.
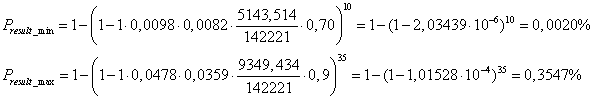
Попробуем теперь подсчитать число знакомств в год, которое требуется для того, чтобы встретить такую девушку с 10% вероятностью:

Как можно видеть, при оптимистичном подходе шанс на удачу, равный 10%, мы получаем, если ежедневно знакомимся примерно с тремя новыми людьми.
Анализ результатов и выводы
Даже прикидочный расчет, произведенный с использованием этой модели, подтверждает близость к истине известного изречения о том, что умных красивых девушек не бывает. Действительно, даже при оптимистичном подходе получается, что умная красивая девушка встречается с частотой примерно 1 на 10000 новых лиц. Поэтому многие их так никогда и не встретят, что равносильно тому, что в их реальности их не существует.
Самым надежными методами увеличения вероятности такого знакомства, в рамках данной модели, являются:
· Существенное снижение пороговых требований.
· Общее увеличение числа знакомств.
· Предпочтение в знакомстве более молодых леди.
Дальнейшие исследования, направленные на развитие данной модели, в первую очередь должны дать количественную оценку фактору k0, а также, возможно, количественно учесть взаимозависимость используемых выборок и внести изменения в основную формулу для вычисления вероятности единственного знакомства. Еще одним из направлений развития является учет специфики конкретных видов знакомств и диверсификация соответствующих формул.
Список литературы
1.
Tristan
Miller “Why I Will Never Have a Girlfriend” http://en.nothingisreal.com/wiki/Why_I_Will_Never_Have_a_Girlfriend
2. Александр Ларионов «Считаем IQ», http://www.bssl.ru/articles/?id=7
3. Орлов А.И. Прикладная статистика, М.: Издательство «Экзамен», 2004. (http://www.aup.ru/books/m163/1_4_2.htm)
4. Федеральная служба государственной статистики. Распределение населения по возрастным группам http://www.gks.ru/bgd/regl/b08_11/IssWWW.exe/Stg/d01/05-02.htm
5. Брачность в России: история и современность, http://www.polit.ru/research/2006/11/02/demoscope261.html
P.s. Если формул не видно, значит
либо с графикой беда, либо статью криворуко скопипастили.
Оригинал на www.probability-asa.narod.ru
Контактный e-mail: probability-asa@ya.ru
Джаббер ведущего теоретика-консультанта: minamikana@jabber.ru